Сила сопротивления

Скорости движения а, давления воздуха в шине б и момента, передаваемого через колесо в

факторов
и определяется экспериментально. Его
средние значения для различных дорог
при нормальном давлении воздуха в шине
составляют 0,01 …0,1.Рассмотрим влияние
различных факторов на коэффициент
сопротивления качению.

Скорость
движения.
При изменении скорости движения в
ин­тервале 0…50 км/ч коэффициент
сопротивления качению изме­няется
незначительно и его можно считать
постоянным в указан­ном диапазоне
скоростей.

При
повышении скорости движения за пределами
указанного интервала коэффициент
сопротивления качению существенно
уве­личивается (рис. 3.15, а)вследствие
возрастания потерь энергии в шине на
трение.

Коэффициент
сопротивления качению в зависимости
от ско­рости движения можно приближенно
рассчитать по
формуле

где—скорость
автомобиля, км/ч.

Тип
и состояние покрытия дороги.
На дорогах с твердым по­крытием
сопротивление качению обусловлено
главным образом деформациями шины.

При
увеличении числа дорожных неровностей
коэффициент сопротивления качению
возрастает.

На
деформируемых дорогах коэффициент
сопротивления ка­чению определяется
деформациями шины и дороги. В этом случае
он зависит не только от типа шины, но и
от глубины образую­щейся колеи и
состояния грунта.

Значения
коэффициента сопротивления качению
при рекомен­дуемых уровнях давления
воздуха и нагрузки на шину и средней
скорости движения на различных дорогах
приведены ниже:

Асфальто-
и цементобетонное шоссе:

в
хорошем состоянии
………………………………. 0,007…0,015

в
удовлетворительном состоянии
…………… 0,015…0,02

Гравийная
дорога в хорошем состоянии …. 0,02…0,025

Булыжная
дорога в хорошем состоянии…… 0,025…0,03

Грунтовая
дорога сухая, укатанная …………..
0,025…0,03

Песок…………………………………………………………..
0,1…0,3

Обледенелая
дорога, лед …………………………. 0,015…0,03

Укатанная
снежная дорога ………………………..
0,03…0,05

Тип
шины.
Коэффициент сопротивления качению во
многом зависит от рисунка протектора,
его износа, конструкции каркаса и
качества материала шины. Изношенность
протектора, уменьше­ние числа слоев
корда и улучшение качества материала
приводят к падению коэффициента
сопротивления качению вследствие
снижения потерь энергии в шине.

Давление
воздуха в шине.
На дорогах с твердым покрытием при
уменьшении давления воздуха в шине
коэффициент сопро­тивления качению
повышается (рис. 3.15, б).На
деформируемых дорогах при снижении
давления воздуха в шине уменьшается
глу­бина колеи, но возрастают потери
на внутреннее трение в шине. Поэтому
для каждого типа дороги рекомендуется
определенное давление воздуха в шине,
при котором коэффициент сопротивле­ния
качению имеет минимальное значение.

Нагрузка
на колесо.
При увеличении вертикальной нагрузки
на колесо коэффициент сопротивления
качению существенно возрастает на
деформируемых дорогах и незначительно
— на до­рогах с твердым покрытием.

Момент,
передаваемый через колесо.
При передаче момента через колесо
коэффициент сопротивления качению
возрастает (рис. 3.15, в)вследствие
потерь на проскальзывание шины в месте
ее контакта с дорогой. Для ведущих колес
значение коэффициента сопротивления
качению на 10… 15 % больше, чем для ведомых.

Коэффициент
сопротивления качению оказывает
существен­ное влияние на расход
топлива и, следовательно, на топливную
экономичность автомобиля. Исследования
показали, что даже не­большое уменьшение
этого коэффициента обеспечивает
ощути­мую экономию топлива. Поэтому
неслучайно стремление конст­рукторов
и исследователей создать такие шины,
при использова­нии которых коэффициент
сопротивления качению будет незна­чительным,
но это весьма сложная проблема.

6.5.Сила упругости. Закон Гука.

При
действии на тело внешних сил, возникает
упругая и неупругая деформация.

П

x

x=0

ри упругой деформации тело после
прекращения действия внешних сил
полностью восстанавливает свою форму
и размеры. При неупругой деформации
форма и размеры тела не восстанавливаются.

Упругая
деформация пружины.

При растяжении пружины (рис 2.14) на
величинуотносительно её равновесного состояния
(х= 0) возникает упругая сила,
которая возвращает пружину в прежнее
положение после прекращения действия
внешней силы. Модуль упругой силы,
возникающей прилинейном растяжении
или сжатии пружины определяется законом
Гука.

,
(2.56)

где– проекция силы упругости на осьx,
знак минус учитывает противоположные
направления силыи перемещения пружины.

Деформация стержня

Стержень длинной lи сечениемSпри действии
силиперпендикулярно его торцам в противоположных
направлениях деформируется (растягивается
или сжимается) (рис 2.15). Деформация
стержня определяется относительной
величиной

(2.57)

где ∆l=l — l
, l—длинна стержня
после деформации.

Рис. 2.15

Опыт показывает, что

,
(2.58)

где α
– коэффициент упругости стержня,

=σ
– нормальное напряжение, измеряемое в(паскаль).

Наряду с коэффициентом упругости aдля характеристики упругих свойств тел
при нормальных напряжениях используютмодуль ЮнгаЕ = 1/a,
который, как и напряжение, измеряется
в паскалях.

Относительное удлинение (сжатие) и
модуль Юнга в соответствии с равенствами
(2.13 и 2.14) определяется из соотношений:

,.
(2.59)

Модуль Юнга равен такому нормальному
напряжению, при котором деформация
стержня Dlравна его первоначальной длинеl.
В действительности при таких напряжениях
происходит разрушение стержня.

Решая уравнение (2.58) относительно F,
и подставляя вместоe=Dl/l,a= 1/Е, получим формулу
для определения силы деформирующей
стержень с сечениемSна
величину

,
(2.60)

где–
постоянный для стержня коэффициент,
который в соответствии с законом Гука
соответствует коэффициенту упругости
стержня при его сжатии и растяжении.

При действии на стержень касательного
(тангенциального) напряжения

силы
F₁ иF₂приложены параллельно противоположным
граням площадьюSпрямоугольного стержня вызываютдеформацию сдвига (рис
2.16).

b

Рис. 2.16

Если действие сил равномерно распределено
по всей поверхности соответствующей
грани, то в любом сечении, параллельном
этим граням, возникает тангенциальное
напряжение.
Под действием напряжений тело деформируется
так, что одна грань сместиться относительно
другой на некоторое расстояниеа. Если
тело мысленно разбить на элементарные,
параллельные рассматриваем граням
слои, то каждый слой окажется сдвинутым
относительно соседних с ним слоев.

При деформации сдвига любая прямая,
первоначально перпендикулярная к слоям,
отклонится на некоторый угол φ. тангенс
которого называется относительным
сдвигом

,
(2.61)

где b– высота грани. При
упругих деформациях угол φ очень мал,
поэтому можно считать, чтои.

Опыт показывает, что относительный
сдвиг пропорционален тангенциальному
напряжению

,
(2.62)

где G– модуль сдвига.

Модуль сдвигазависит только от свойств материала и
равен тангенциальному напряжению при
угле φ = 45˚. Модуль сдвига так же, как и
модуль Юнга измеряется в паскалях (Па).
Сдвиг стержня на уголвызывает сила

=GSφ,
(2.63)

где
G·S– коэффициент упругости стержня при
деформации сдвига.

Расчет сопротивления последовательных резисторов

Cила тока: формула

При последовательном сопротивлении нескольких резисторов соответственно увеличивается эквивалентная величина. Расчет сопротивления нескольких элементов, соединенных между собой последовательно, проводится за счет суммирования номиналов каждого элемента. Например, при соединении нескольких элементов, которые соединены в одну цепь последовательно, величина электрического сопротивления будет равной сумме уровня противодействия каждого из резисторов. Формула имеет одинаковый вид для любого количества резисторов.

Как найти сопротивление формула для последовательной цепи

Если заменить в последовательной цепи один из элементов, то соответственно изменится уровень противодействия направленному движению частиц в этой цепи. Это также повлечет изменение силы тока.

Резистор

Уравнение координаты и скорости при свободном падении

Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:

Уравнение скорости при свободном падении:

v_y = v_0y + g_yt

Полезные факты

• В момент падения тела на землю y = 0.
• В момент броска тела от земли y = 0.
• Когда тело падает без начальной скорости (свободно) v = 0.
• Когда тело достигает наибольшей высоты v = 0.

Построение чертежа

Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.

План построения чертежа

• Чертится ось ОУ. Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
• Отмечаются начальная и конечная координаты тела (y и y).
• Указываются направления векторов. Нужно указать направление ускорения свободного падения, начальной и конечной скоростей.

Уравнение скорости:

–v = v – gt_пад

Уравнение координаты:

Уравнение скорости:

–v = v – gt

Уравнение координаты:

Тело подбросили от земли, на одной и той же высоте оно побывало дважды

Чертеж:

Интервал времени между моментами прохождения высоты h:

∆t = t₂ – t₁

Уравнение координаты для первого прохождения h:

Уравнение координаты для второго прохождения h:

Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ. Пример №5

Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?

Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?

Из условия задачи начальная скорость равна 0, а начальная координата — 50.

Поэтому:

Через 3 с после падения тело окажется на высоте 5 м.

Пример задачи на законы Ньютона

Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.

Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.

Решение:  

Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.

На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.

По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.

Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.

Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.

Решение:

По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.

Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.

Силы сопротивления при больших скоростях

Сила сопротивления, оказывающая воздействие на движущиеся предметы с малой скоростью, зависит от нескольких внешних факторов. К таким условиям относятся:

• вязкость жидкости;
• скорость перемещения тела;
• линейные размеры движущегося предмета.

В условиях больших скоростей характер действия силы сопротивления несколько изменяется. Законы вязкого трения в этом случае не применяются для воздуха и воды. Если скорость предмета составляет 1 сантиметр в секунду, то данные факторы учитываются лишь тогда, когда тела обладают крошечными размерами, измеряемыми в миллиметрах.

Примечание

Если пловец ныряет в воду, то на него будет действовать сила сопротивления. Однако в данном случае закон вязкого трения не будет действовать.

Объект, двигаясь с малой скоростью в водной среде, плавно обтекается жидкостью. Сила сопротивления в данном случае будет рассчитываться, как сила вязкого трения. Если скорость большая, то с задней части перемещающегося тела наблюдается более сложное движение жидкости с образованием необычных по форме фигур, вихрей, колец. Картина таких струек будет постоянно изменяться. Движение такого характера называется турбулентным. Турбулентное сопротивление все еще будет определяться скоростью и размерами тела, но не так, как при вязком сопротивлении. В данном случае сила рассчитывается пропорционально квадрату скорости и линейным размерам предмета. Вязкость водной среды более не имеет решающего значения, определяющая функция переходит к показателю плотности.

Сила турбулентного сопротивления рассчитывается по формуле:

\($$F=p\times V^{2}\times L^{2}$$\)

Вес тела

Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!

Формулы определения веса нет. Обозначается эта силы буквой .

Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.

Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.

Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!

Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила

Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!. Перегрузка — отношение веса к силе тяжести

Перегрузка — отношение веса к силе тяжести

Что такое сила сопротивления

При совершенно любом движении будет фиксироваться появление между поверхностями тел или в среде, где оно осуществляется, сил сопротивления. Второе свойственное им название — силы трения.

Определение

Сила трения — сила, которая появляется в момент передвижения одного тела вдоль другого либо в какой-то среде, ведущая к замедлению действия.

Препятствие движению объясняется тем, что силы трения имеют противоположное направление, и в момент, когда движущая сила и силы сопротивления уравновесятся, скорость станет равна 0.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Схематически действие силы трения можно представить на рисунке:

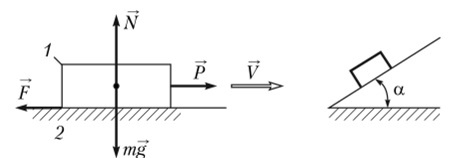
Изображенное здесь тело массой m лежит на ровной поверхности, и на него действуют сила тяжести и уравновешивающая ее сила опоры (N). Направления этих двух сил противоположные, однако, обе — перпендикулярны поверхности.

Сила опоры по своей величине определяется по формуле:

\(N=m\times g\)

С позиций механики понятно, что для того, чтобы сдвинуть это тело с места, необходимо приложить усилие (P), превосходящее силу трения (F).

Определение

Основателем закона трения считается француз Гийом Амонтон. Согласно его постулатам, F_тр пропорциональна давлению, которое тело оказывает на опору либо на другое тело. Кроме этого, она определяется физическими свойствами контактирующих материалов, но не зависит от величины поверхности соприкосновения.

Как любая другая, сила трения измеряется в Ньютонах (Н).

Как найти силу сопротивления

Как видно из формулы, величина полного гидродинамического сопротивления прямо пропорциональна величине миделевого сечения. При плавании человека величина миделевого сечения постоянно изменяется. Наименьшая проекция будет в том случае, если тело занимает в воде горизонтальное положение.

Внимание

Величину миделевого сечения необходимо учитывать не только при выборе рационального положения тела, но и при выполнении рабочих и подготовительных движений. Пловец продвигается вперед, опираясь конечностями о воду и отталкиваясь от нее. Отталкивания будут тем более эффективными, чем больше они будут вызывать сопротивление своему движению, которое зависит от величины миделевого сечения.

Падение тел в воздухе.

Пока
скорость падающего тела еще мала, невелика и сила сопротивления воздуха; но по
мере того, как возрастает скорость падения, эта сила быстро растет. При
некоторой скорости сила  становится равной по модулю силе , и дальше тело
падает равномерно. Скорость такого падения называют предельной скоростью
падения. Предельная скорость тем больше, чем сильнее разрежен воздух.
Поэтому тело, падающее с очень большой высоты, может в разреженных слоях
атмосферы приобрести скорость, большую предельной скорости для нижних
(плотных) слоев. Войдя в нижние слои атмосферы, тело снизит свою скорость до
значения предельной скорости для нижних слоев.

Упражнение: 68.1.
Деформировано ли тело, падающее с предельной скоростью?

Предельная скорость
падения зависит, помимо плотности атмосферы, от формы и размеров тела и от
силы притяжения тела Землей. Тела малого размера, например мелкие капли воды
(туман), пылинки, снежинки, быстро достигают своей предельной скорости (порядка
миллиметра в секунду и меньше) и затем с этой малой скоростью опускаются вниз.
Свинцовый шарик массы 10 г достигает при падении с достаточной высоты
предельной скорости 40 м/с. Капли дождя падают со скоростью, обычно не
превышающей 7—8 м/с; чем меньше капля, тем меньше и скорость ее падения; если
бы капли дождя падали в безвоздушном пространстве, то при падении на землю с
высоты 2 км они достигали бы, независимо от их размеров, скорости 200 м/с;
такой же скорости при падении с той же высоты в безвоздушном пространстве
достигло бы и всякое другое тело. При такой скорости удары капель дождя были
бы весьма неприятны!

Различие
в предельной скорости разных тел одинаковой формы, но разных размеров
объясняется зависимостью сопротивления среды от размеров тела. Оказывается,
что сопротивление приблизительно пропорционально площади поперечного сечения
тела. При одной и той же форме тела из данного материала площадь его
поперечного сечения, а значит и сила сопротивления воздуха, растет с
увеличением размеров медленнее, чем сила тяжести: площадь поперечного сечения
растет как квадрат размера, а сила тяжести — как куб размера тела. Например,
чем больше авиационная бомба, тем больше ее предельная скорость и с тем большей
скоростью она достигает земли.

Рис. 93. Сопротивление воздуха при
движении тела каплевидной формы в 30 раз меньше сопротивления при движении
круглой пластинки и в 5 раз меньше сопротивления при движении шарика того же
поперечного сечения

Наконец,
сопротивление воздуха сильно зависит и от формы тел (рис. 93, см. также §
190). Фюзеляжу самолета придают специальную обтекаемую форму, при которой
сопротивление воздуха мало. Наоборот, парашютист должен достигать земли с
небольшой скоростью. Поэтому парашюту придают такую форму, при которой сопротивление
воздуха его движению было бы возможно больше. Предельная скорость падения
человека с раскрытым парашютом составляет 5—7 м/с. Достижение предельной
скорости парашютистом происходит иначе, чем при простом падении тела. Вначале
парашютист падает с закрытым парашютом и ввиду малого сопротивления воздуха
достигает скорости в десятки метров в секунду. При раскрытии парашюта сопротивление
воздуха резко возрастает и, превосходя во много раз силу тяжести, замедляет
падение до предельной скорости.

Сопротивление
воздуха изменяет и характер движения тел, брошенных вверх. При движении тела
вверх и сила земного притяжения, и сила сопротивления воздуха направлены вниз.
Поэтому скорость тела убывает быстрее, чем это происходило бы в отсутствие
воздуха. Вследствие этого тело, брошенное вверх с начальной скоростью , не достигает
высоты  (как это было бы
при отсутствии сопротивления) и уже на меньшей высоте начинает падать обратно.
При падении сопротивление воздуха уменьшает нарастание скорости. В результате
тело, брошенное вверх, всегда возвращается назад с меньшей скоростью, чем оно
было брошено. Таким образом, при падении на землю средняя скорость движения
меньше, чем при подъеме, и поэтому время падения на землю больше времени
подъема.

Влияние
сопротивления воздуха особенно велико при больших скоростях (так как сила
сопротивления быстро растет со скоростью). Так, например, при выстреле из винтовки
вертикально вверх пуля, вылетающая с начальной скоростью 600 м/с, должна была
бы в отсутствие воздуха достичь высоты, равной

В
действительности пуля достигает высоты только 2—3 км. При падении обратно
скорость пули возрастает лишь до 50—60 м/с. С этой предельной скоростью пуля и
достигает земли.

Примеры решения задач

Пример

Задание. Проводящий шар, имеющий радиус А окружён тонкой проводящей оболочкой радиуса B (рис.1).
Пространство между телами заполнено однородным и изотропным веществом, удельное сопротивление которого $\rho$.
Каково сопротивление пространства между электродами?

Решение. За основу решения задачи примем формулу:

$$R=\int_{1}^{2} \rho \frac{d l}{S}(1.1)$$

где положим:

$$d l=d r ; S=4 \pi r^{2}(1.2)$$

Интегрирование выражения (1.1) проведем от A до B:

$$R=\int_{A}^{B} \rho \frac{d r}{4 \pi r^{2}}=-\left.\frac{\rho}{4 \pi} \frac{1}{r}\right|_{A} ^{B}=\frac{\rho}{4 \pi} \cdot \frac{B-A}{B \cdot A}$$

Ответ. $R=\frac{\rho}{4 \pi} \cdot \frac{B-A}{B \cdot A}$

Слишком сложно?

Формула сопротивления не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Какое количество витков проволоки (n) (удельное сопротивление ее равно
$\rho$=100 мк Ом•м, диаметр d=1 см) требуется накрутить
на фарфоровый цилиндр, имеющий радиус A=1 см, для того чтобы получить сопротивление R=8 Ом?

Решение. Основой для решения задачи будет формула для сопротивления вида:

$$R=\rho \frac{l}{S}(2.1)$$

Длину одного витка проволоки можно вычислить как:

$$l_{1}=2 \pi \cdot A(2.2)$$

Следовательно, длина всей проволоки (l) равна:

$$l=n \cdot 2 \pi \cdot A(2.3)$$

Площадь поперечного сечения проволоки (S):

$$S=\pi \frac{d^{2}}{4}(2.4)$$

Подставим (2.4), (2.3) в выражение (2.1)

$$R=\rho \frac{n \cdot 2 \pi \cdot A}{\pi \frac{d^{2}}{4}}=8 \rho \frac{n \cdot A}{d^{2}}(2.5)$$

Из формулы (2.6) получим искомое число витков:

$$n=\frac{R d^{2}}{8 \rho A}$$

Переведем единицы всех величин из данных задачи в систему СИ, имеем:
$\rho$=100 мк Ом•м=100•10-6 Ом•м,d=1 см=10-2 м,
A=1 см=10-2 м проведем вычисления:

$$n=\frac{8 \cdot\left(10^{-2}\right)^{2}}{8 \cdot 10^{-4} \cdot 10^{-2}}=100$$

Ответ. n=100

Читать дальше: Формула внутренней энергии.

Направление силы трения

Сила трения скольжения всегда направлена противоположно скорости относительного движения соприкасающихся тел

Важно помнить, что на каждое из соприкасающихся тел действует своя сила трения

Бывают ситуации, когда сила трения не препятствует движению, а совсем наоборот.

Представьте, что на ленте транспортёра лежит чемодан. Лента трогается с места, и чемодан движется вместе с ней. Сила трения между лентой и чемоданом оказалась достаточной, чтобы преодолеть инерцию чемодана, и эти тела движутся как одно целое. На чемодан действует сила трения покоя, возникающая при взаимодействии соприкасающихся поверхностей, которая направлена по ходу движения ленты транспортёра.

 Если бы лента была абсолютно гладкой, то чемодан начал бы скользить по ней, стремясь сохранить своё состояние покоя. Напомним, что это явление называется инерцией.

Сила трения покоя, помогающая нам ходить и бегать, также направлена не против движения, а вперёд по ходу перемещения. При повороте же автомобиля  сила трения покоя и вовсе направлена к  центру окружности. 

Для того чтобы понять, как направлена сила трения покоя, нужно предположить, в каком направлении стало бы двигаться тело, будь поверхность идеально гладкой. Сила трения покоя в этом случае будет направлена как раз в противоположную сторону. Пример, лестница у стены.

Формулы для определения силы тяги

Согласно второму закону Ньютона, сумма сил, воздействующих на движущееся тело, равна массе \(m\), умноженной на ускорение \(a\). Универсальной формулы, подходящей для любого сочетания сил, не существует. Чаще всего силу тяги находят с помощью общей формулы\( F_т-\;F_{с}=m\;\times\;a\), где \(F_т\) — сила тяги, \(F_{с}\) — силы сопротивления.
При решении конкретной задачи силы, воздействующие на тело, схематически изображают в виде векторов. На схеме:

• сила тяжести mg;
• сила реакции опоры \(N\);
• сила трения\( F_{тр}\);
• сила тяги \(F\). 

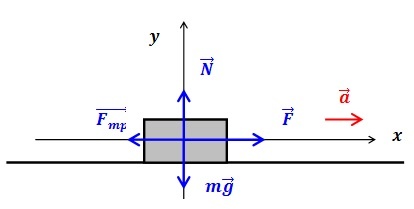
При нахождении тела на горизонтальной поверхности сила тяжести и сила реакции опоры уравновесят друг друга. Но если транспортное средство движется в гору или под гору, придется учесть влияние уклона. Тогда формула может выглядеть так: \(F_т-\;F_с-\;mg\;\times\;\sin\alpha=m\;\times\;a.\)

Работа A, которую должна совершить сила тяги, сдвигая тело, связана с ней соотношением \(A\;=\;F\;\times\;s\). \(s\) здесь — расстояние, на которое тело переместилось.

Формула через мощность

Полезную механическую мощность \(N\) можно вычислить по формуле \(N=F_т\;\times\;v\), где \(v\) — скорость. Для определения силы тяги нужно разделить мощность на скорость: \(F_т\;=\;\frac N v.\)

Расчет падения напряжения

Любой проводник, кроме сверхпроводников, имеет сопротивление. Поэтому при достаточной длине кабеля или провода происходит падение напряжения. Нормы ПЭУ требуют, чтобы сечение жилы кабеля было таким при котором падение напряжения составляло не более 5%.

В первую очередь это касается низковольтных кабелей малого сечения. Расчет падения напряжения выглядит следующим образом:

R = 2*(ρ * L) / S

U пад = I * R

U % = (U пад / U лин) * 100

2 – коэффициент, обусловленный тем, что ток течет обязательно по двум жилам

R – сопротивление проводника, Ом

ρ — удельное сопротивление проводника, Ом*мм 2 /м

S – сечение проводника, мм 2

U пад – напряжение падения, В

U % — падение напряжения по отношению к U лин,%

Таблица 9. Удельное сопротивление распространенных металлических проводников (+)

Формула

Общее электросопротивление проводника можно найти по представленной выше формуле. Что касается нахождения показаний для активной, реактивной, отрицательной и удельной разновидности, есть свои специальные формулы. Все они представлены в соответствующей схеме далее с обозначениями.

Формулы, используемые для расчета значения проводника

Электросопротивление в электродинамике является электротехнической величиной, характеризующей способность металла препятствовать электрическому току. При расчетах используется буква R, вне зависимости от того, какое сопротивление изучается и подсчитывается. Формул для нахождения величины множество. В основном используется R=U/I.

Емкостное сопротивление

Оно имеет иную природу, чем индуктивное. Это понятие удобно проиллюстрировать на примере электрической цепи, состоящей из источника питания, клеммы которого соединены с обкладками конденсатора. Сразу после подключения на них будет постепенно накапливаться заряд, создавая ток в цепи.

После достижения предельной величины, которая определяется ёмкостью детали, ток не будет проходить по цепи. Если после этого отключить провода от клемм, а затем последние соединить, то между ними начнётся перемещение зарядов до тех пор, пока разность потенциалов станет равной нулю.

Если к конденсатору подключить источник переменного тока, то будет происходить следующее. С увеличением разности потенциалов заряд на обкладках конденсатора будет расти. Когда напряжение перейдёт в фазу уменьшения, накопленный заряд начнёт стекать с них, образуя ток противоположного направления. Затем разность потенциалов станет отрицательной, но по абсолютной величине будет расти до максимального значения. При этом конденсатор начнет вновь заряжаться, но при этом знак поступающих зарядов будет не такой, который был раньше.

Когда напряжение начнёт увеличиваться (уменьшаясь по абсолютной величине), заряд с обкладок конденсатора будет стекать. Когда разность потенциалов у источника достигнет нуля и продолжит увеличиваться, начнётся новый цикл изменений.

На каждом этапе описанной ситуации ток с обкладок конденсатора будет иметь направление противоположное тому, которое порождается переменной разностью потенциалов источника питания.

Происходящее таким образом уменьшение силы тока представляет собой физический смысл ёмкостного сопротивления. Оно обозначается буквами ХС и рассчитывается по формуле:

XС = 1/(w×C) = 1/(2π×f×C), где

• C — ёмкость используемого конденсатора;
• w — круговая частота переменного тока;
• π — число «пи»;
• f — частота переменного тока.

В рассматриваемом случае изменения тока отстают от напряжения.